Klassifizierung
Cat or no cat?
Detail aus
Jan de Beer
The Annunciation
ca. 1520
Einführung
In der Statistik und im Machine Learning ist eine Klassifizierung eine Aufgabe, bei der identifiziert werden soll, zu welcher Kategorie, aus einem finiten Satz von Kategorien, eine neue Beobachtung gehört. Dies geschieht auf Basis eines Trainingsdatensatzes, der Beobachtungen enthält, deren Kategorien bekannt sind. Eine Klassifizierung läuft im allgemeinen Supervised (Überwachtes Lernen) oder Semi-Supervised (Teilüberwachtes Lernen) ab. Die korrespondierende unüberwachte Prozedur ist die Clusteranalyse. Bei dieser werden die Daten in Kategorien, basierend auf Maßstäben inhärenter Ähnlichkeit oder Distanz, gruppiert.
Es gibt unendlich viele Anwendungsgebiete für Klassifizierungen, einige Beispiele sind die Spracherkennung, Erkennung von Handschrift, Empfehlungsdienste (Recommender System), Suchmaschinen, Entwicklung von neuen Medikamenten oder Computer Vision.
Begriffsabgrenzung. Im Deutschen wird für die Einordnung von Objekten in bestehende Klassen der Begriff ‚Klassieren‘ verwendet, meistens liest man jedoch im Zusammenhang mit Machine Learning den Begriff ‚Klassifizieren‘, der auch hier verwendet wird.
Inhalt. In diesem Artikel werden verschiedene Herangehensweisen für das Klassifizieren von Objekten aufgezeigt. Neben Varianten der Klassifizierung werden die populärsten Lernalgorithmen und Metriken vorgestellt und bei der Entwicklung eines Machine Learning Modells wichtige Punkte, wie die Kalibrierung, Konfidenzintervalle und die Interpretation des Modells besprochen.
Varianten der Klassifizierung
Es gibt verschiedene Varianten der Klassifizierung, die sich in der Art der Zielvariablen unterscheiden.
Bei der One-Class Klassifizierung sollen Objekte einer Klasse identifiziert werden. Das Modell lernt aus einem Trainingssatz, in dem nur Instanzen dieser Klasse vorkommen. Diese Art der Klassifizierung wird beispielsweise in der Überwachung von Kernkraftwerken verwendet.
Ein Sonderfall der One-Class Classification ist die Anomaly Detection. Hier sollen außergewöhnliche Ereignisse erkannt werden, die außerhalb der für diese Daten angenommenen Wahrscheinlichkeitsverteilung fallen. Für die Anomaly Detection werden Hidden-Markov-Modelle, One-Class Support Vector Machines und Bayesian Networks verwendet und sie kann Supervised, Unsupervised oder Semi-Supervised ablaufen.
Bei der Binären Klassifizierung sollen neue Beobachtungen einer von zwei möglichen Kategorien zugeordnet werden. Diese Art der Klassifizierung ist sehr häufig und wird beispielsweise für die Erkennung von Spam-E-Mails (Spam/kein Spam) oder Krankheiten (krank/gesund) verwendet. Die Grundklasse ist oft die negative Klasse, die mit einem Label 0 versehen wird, die seltenere Klasse, nach der gesucht wird, ist die positive Klasse, die das Label 1 zugewiesen bekommt.
Die Mehrklassen Klassifizierung weist einer neuen Beobachtung eine Kategorie aus einem Satz von drei oder mehr möglichen Kategorien zu. Alle Mehrklassen Klassifizierungen können mit Hilfe eines Wrappers auf eine binäre Klassifizierung reduziert werden. Der am häufigsten verwendete Wrapper ist der One-Vs-All-Wrapper, der den Klassifikator jeweils einmal für jede vorhandene Klasse trainiert.
Bei der Multilabel Klassifizierung werden einer Beobachtung mehrere Kategorien zugewiesen. Beispiele für Lernalgorithmen, die damit umgehen können, sind K-Nearest Neighbors und Decision Trees.
Es gibt eine sehr große Auswahl von Lernalgorithmen, die für eine Klassifizierung verwendet werden können und eine ebenso große Auswahl an Evaluierungsmöglichkeiten. Ich beschreibe hier eine kleine Auswahl der bewährtesten Methoden für Anwendungen mit strukturierten tabellarischen Daten. Viele der vorgestellten Methoden werden jedoch genauso auch für die Klassifizierung unstrukturierten Daten, wie Bilder, Sprache oder Text verwendet. Die meisten Lernalgorithmen eignen sich für alle Formen der Klassifizierung, nur für die Multilabel-Klassifizierung müssen Anpassungen vorgenommen werden.
Algorithmen für Klassifizierungsaufgaben
Die meisten der hier vorgestellten Algorithmen können sowohl für Regressionsanalysen als auch für die Klassifizierung verwendet werden. Es gibt nicht den einen perfekten Lernalgorithmus für eine Aufgabe, daher wird der beste Lernalgorithmus für die vorliegende Aufgabe am besten im Experiment gefunden (No free Lunch!). Daher kann es sinnvoll sein, mehrere Algorithmen zu testen, um zu sehen, welcher die beste Performance für das vorliegende Problem zeigt. Dann kann entweder einfach der beste Algorithmus weiterentwickelt werden oder es kann ein Ensemble der besten Algorithmen eingesetzt werden.
Logistische Regression
Die Logistic Regression ist eine binäre Klassifizierungsmethode. Das resultierende Modell ist parametrisch, was bedeutet, dass die Daten durch eine Funktion repräsentiert werden. Anhand er Koeffizienten (Gewichte) der Gleichung kann das Modell interpretiert werden. Je größer das Gewicht, desto wichtiger die Variable. Für eine korrekte Interpretation wird vorausgesetzt, dass die Beobachtungen unabhängig voneinander sind und es keine Kollinearität zwischen den Variablen gibt. Im Gegensatz zur Linearen Regression müssen die Residuen nicht normalverteilt sein.
Das Modell wird über eine Kostenfunktion, die mit Hilfe eines Optimierungsalgorithmus iterativ minimiert wird, approximiert.
Neue Beobachtungen werden klassifiziert, in dem die Variablen neuer Beobachtungen in die Funktion eingesetzt werden und das Ergebnis berechnet wird. Die Ausgabe ist die Wahrscheinlichkeit P, dass eine Beobachtung zur positiven Klasse gehört. Oft wird in einem weiteren Schritt anhand eines Schwellenwertes die Wahrscheinlichkeit in ein Klassenlabel umgewandelt.
Der Datensatz für eine Logistische Regression sollte in der Vorbereitung (Preprocessing) immer skaliert werden und bei Variablenpaaren, die miteinander korrelieren, sollte eine davon entfernt werden.
Bei der Anwendung in Scikit-Learn gibt es die Möglichkeit, zwischen verschiedenen Optimierungsalgorithmen (Solver) zu wählen. Dieser Parameter sollte immer auf den vorliegenden Fall angepasst werden. Weitere wichtige Hyperparameter sind die „penalty„, die die Art der Regularisierung vorgeben und „C„, mit dem die Stärke der Regularisierung bestimmt wird. Eine weitere Implementierung testet automatisch verschiedene Hyperparameter-Kombinationen in einer Kreuzvalidierung.
Mehr zu Hyperparametern, Attributen und Anwendung in der Beschreibung des Lernalgorithmus auf den Seiten von Scikit-Learn hier.
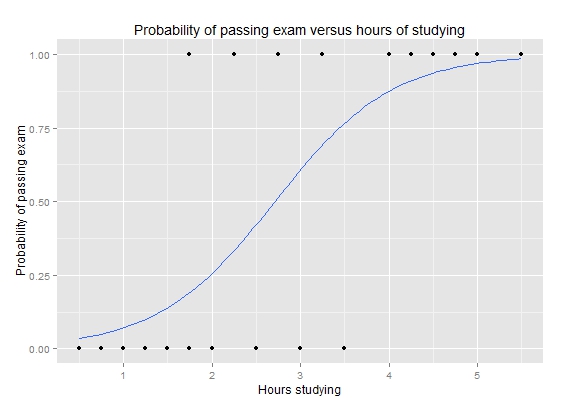
Logistische Kurve (Wikipedia)
K-Nearest-Neighbors (KNN)
KNN ist eine nichtparametrische Methode zur binären und Mehrklassen-Klassifikation, die auch für Regressionsaufgaben verwendet werden kann.
Es werden keine Annahmen über die Verteilung der Daten getroffen, was ihn zu einer guten Wahl machen, wenn wenig über die Eigenschaften des Datensatzes bekannt ist.
Der Algorithmus wird häufig in Online Empfehlungsdiensten oder zur Entdeckung von Mustern in Kreditkartenkäufen verwendet.
Die Methode des KNN ist, dass, statt eine Funktion zu approximieren, der komplette Trainingssatz abgespeichert wird (Lazy Learner). Dies verkürzt die Trainingsphase, da in dieser einfach die Feature Vektoren und Klassen-Labels abgespeichert werden, bedeutet aber auch, dass eine relativ große Menge an Trainingsdaten zur Verfügung gestellt werden sollte. Neue Daten hinzuzufügen ist kein Problem und kann jederzeit erfolgen, was die Methode ideal für Echtzeitanwendungen macht.
Soll eine neue Beobachtung klassifiziert werden, wird deren Ähnlichkeit (Beispielsweise durch Euklidische Distanz) zu den gespeicherten Instanzen berechnet und die häufigste Klasse der nächsten Nachbarn wird als Klasse ausgegeben. Die Entfernungen können auch gewichtet eingehen, hierfür wird die invertierte Distanz verwendet.
Da für jede neue Instanz der gesamte Datensatz ausgewertet wird, um eine Vorhersage zu machen, bedeutet dies hohe Kosten für Zeit und Speicherplatz. Der Algorithmus ist nicht robust gegen Ausreißer, da jegliche Information aus dem Datensatz und nicht aus einer Generalisierung kommt. Hier kann es helfen, die Anzahl k der Nachbarn zu erhöhen oder Ausreißer im Preprocessing zu behandeln. Die Daten sollten im Preprocessing auf jeden Fall skaliert werden, wenn Euklidische oder Manhattan Distanz verwendet werden. Auch fehlende Werte müssen entfernt werden, diese können hier beispielsweise mit dem Mittelwert gefüllt werden.
Die Ausgabe von Wahrscheinlichkeiten der Klassenzugehörigkeit ist möglich, allerdings müssen diese kalibriert werden.
Bei der Anwendung in Scikit-Learn ist der wichtigste Hyperparameter die Anzahl der Nachbarn k, die in die Bewertung eingehen sollen. Dieser Wert wird am besten experimentell in einer Kreuzvalidierung ermittelt. Je höher die Anzahl der Nachbarn, die miteinbezogen werden, desto höher ist das Bias und desto niedriger die Varianz des Modells. Die Komplexität des Modells sinkt mit steigender Anzahl der Nachbarn k. Mehr zum Lernalgorithmus in Scikit-Learn hier.
Entscheidungsbäume
Entscheidungsbäume sind eine nichtparametrische Methode zur grafischen Darstellung eines Regelsatzes. Sie sind die Grundlage für Modelle wie Random Forest oder Boosted Decision Trees.
Ein Entscheidungsbaum besteht aus Wurzelknoten, inneren Knoten und Blättern. Die Knoten repräsentieren eine logische Regel für das Treffen einer Entscheidung, in den Blättern werden die Ergebnisse repräsentiert.
Ein bekannter Lernalgorithmus für die Erzeugung von Entscheidungsbäumen ist Classification and Regression Trees (CART). CART Modelle unterscheiden sich von anderen Modellen darin, dass sie nicht nur kategorische, sondern auch reelle Variablen verarbeiten können. Bei kategorischen Variablen werden die Entscheidungen anhand der Kategorie getroffen, reelle Variablen werden an einem Schwellenwert diskretisiert. Die Repräsentation der Daten ist ein binärer Entscheidungsbaum, das heißt, jeder Regelausdruck kann nur eine von zwei Werten annehmen.
Die Regeln lernt der Algorithmus induktiv aus dem gegebenen Trainingsdatensatz. Dafür wird für jeden Knoten diejenige Variable gefunden, die die Beobachtungen am saubersten in die gesuchten Klassen aufteilen kann.
Damit wird der Datensatz Schritt für Schritt immer weiter aufgeteilt, bis in jeder Teilmenge nur noch Objekte einer Klasse vorhanden sind. Als Maß für die Güte der Teilung werden der Gini-Koeffizient oder Information Gain verwendet.
Ist der Baum erstellt, kann eine neue Beobachtung klassifiziert werden, indem der Baum von der Wurzel bis in ein Blatt durchlaufen wird und an jedem Knoten anhand des Wertes der Variablen im Knoten und der Beobachtung entschieden wird, welcher Knoten als nächstes ausgewählt wird.
Der fertige Baum kann als Grafik oder als Satz von Regeln abgespeichert werden.
Wird nur ein einzelner Baum verwendet, kommt es höchstwahrscheinlich zu einem Overfitting, da er den Feature-Raum anhand jedes einzelnen Features perfekt aufteilt und dabei nicht generalisiert. Das Modell lernt nicht nur die tatsächlichen Beziehungen in den Trainingsdaten, sondern auch das Rauschen. Damit ist die Varianz sehr hoch, weil die gelernten Parameter sehr stark mit den gegebenen Daten variieren. Im Extremfall gibt es für jede Beobachtung ein Blatt mit der entsprechenden Klasse. Dies kann mit einer Beschränkung der Tiefe des Baumes verhindert werden, was wiederum das Bias erhöhen kann.
Um das Problem zu umgehen, können mehrere Bäume in einem Ensemble verwendet werden. Beispiele für Ensembles aus Entscheidungsbäumen sind Random Forest und Boosted Decision Trees. Diese zeigen eine hervorragende Performance auf vielen verschiedenen Problemen inklusive nichtlinearer Probleme.
Random Forests sind random, weil für jeden Baum ein zufällig gewählter Teil der Beobachtungen und zufällig gewählte Subsets von Features verwendet werden. Nachdem jeder Baum seine Vorhersagen gemacht hat, werden diese gemittelt. Dieser Prozess der Zufallsauswahl und dem Mitteln der Ergebnisse wird Bagging (Kurz für Bootstrap Aggregating) genannt.
Einzig bei der Interpretation gibt es Nachteile; ein einzelner Baum kann grafisch dargestellt werden und ist einfach zu interpretieren, dies trifft nicht mehr auf das Ensemble zu.
Ein großer Vorteil ist, aufgrund der Lernweise, das eine Feature Selection im Modell integriert ist und sogenannte Features Importances zur Interpretation ausgegeben werden können. Auch bei Random Forest kann Kollinearität ein Problem darstellen. Sind zwei Variablen stark kollinear, wird eine der Variablen auf Kosten der anderen höher gewichtet werden, auch wenn beide gleich wichtig sind.
Bei der Anwendung von Entscheidungsbäumen müssen die Daten nur wenig vorbereitet werden; der Algorithmus kann gut mit unskalierten Daten und Ausreißern umgehen. Wird mit Scikit-Learn gearbeitet, sollten die kategorischen Variablen kodiert werden, dies ist jedoch nicht immer nötig, manche Implementierungen, wie H2O können kategorische Variablen direkt verarbeiten.
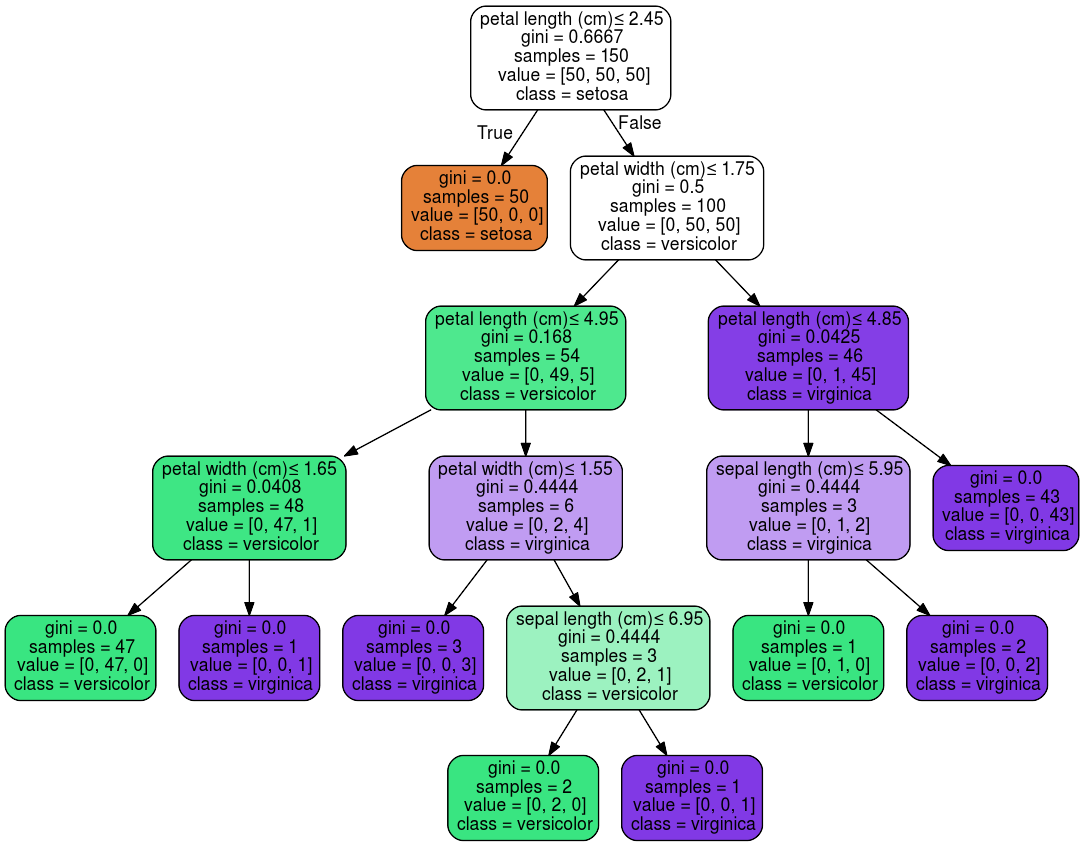
Grafische Darstellung eines Entscheidungsbaumes aus Scikit-Learn für eine Klassifizierung verschiedener Arten der Gattung Iris.
Support Vector Machines (SVM)
SVM ist ein nichtparametrischer, linearer Algorithmus für binäre Klassifizierungen und Regressionsanalysen, wobei er hauptsächlich als Klassifikator verwendet wird. Auch Mehrklassenklassifikationen sind damit möglich.
SVM wird beispielsweise gerne für die Gesichtserkennung eingesetzt, wie auch für die Kategorisierung von Texten oder Bildern. Auch in der Bioinformatik wird er oft verwendet, hier untere anderen für die Klassifizierung von Krebsarten oder Proteinen.
Das Ziel einer Klassifizierung mit SVM ist es, im Feature-Raum eine Entscheidungsgrenze zu ziehen, die die Objekte nach Klassenzugehörigkeit trennt. Dabei sollen Klassen, die trennbar sind, komplett getrennt werden, und sich überlappende Klassen so getrennt werden, dass der Fehler minimal gehalten wird. Je nach Dimensionalität der Daten kann diese Grenze eine Gerade, Ebene oder Hyperebene sein, die die Klassen linear trennt.
Da es unendlich viele mögliche Entscheidungsgrenzen gibt, die die Klassen im Raum trennen können, wird zur Eingrenzung eine weitere Bedingung eingeführt, die besagt, dass die beste Grenze diejenige ist, die die beiden Klassen mit dem größten leeren Bereich beidseitig dieser trennen kann. Dieser Bereich wird „Margin“ („Rand“) genannt. Dieser definiert sich über den kürzesten Abstand der Ebene zu denen ihr am nächsten gelegenen Datenpunkten (= Länge der Lotgeraden).
Die gefundene Grenze ist somit nur von denen ihr am nächsten gelegenen Vektoren abhängig, die ihre Lage beschreiben, weswegen das trainierte Modell nur diese Stützvektoren abspeichert.
Um neue Beobachtungen zu klassifizieren, kann anhand der Gleichung für die Grenze bestimmt werden, auf welcher Seite der Ebene sich das Objekt befindet.
Da Daten in der Realität meistens nicht sauber trennbar sind, und sich die Klassen überlappen, wird in der Praxis ein sogenannter „Soft Margin“ verwendet. Dafür wird die Randbedingung für die Maximierung der Margin aufgeweicht. Dies bedeutet, dass falsche Klassifizierungen einzelner Beobachtungen nun erlaubt sind, aber dennoch bestraft werden. Mit dieser Methode können auch Ausreißer das Modell nicht mehr verzerren. Das Bias des Modells wird erhöht und die Varianz gesenkt.
Zusätzlich werden neue Variablen eingeführt (Schlupfvariablen/Slack Variables), die die Flexibilität der Margin erhöhen. Dies sind Variablen, die für die Lösung eines Problems eingeführt werden, deren Wert aber irrelevant ist. Sie sollen helfen, eine Überanpassung des Modells zu vermeiden und die Zahl der Stützvektoren niedrig zu halten.
Kernel-Trick: Können die Daten im Feature-Raum nicht linear getrennt werden, werden der Vektorraum und die sich darin befindlichen Vektoren der Trainingsdaten in einen höherdimensionalen Raum überführt, bis sie durch eine Hyperebene linear getrennt werden können.
Der SVM Algorithmus wird im Allgemeinen nicht overfitten und er kann gut mit Ausreißern umgehen.
Der Lernalgorithmus erwartet numerische Eingabevariablen, was bedeutet, dass kategorische Variablen am besten in binäre Dummy-Variablen umgewandelt werden, zum Beispiel mit dem OneHotEncoder von Scikit-Learn oder mit pandas.get_dummies.
Zudem ist eine Skalierung der Daten sinnvoll, damit die größerwertigen Variablen im Datensatz nicht dominieren.
Bei der Implementierung in Scikit-Learn ist der Hyperparameter C von Bedeutung, der die Flexibilität der Margin über alle Dimensionen bestimmt. Wenn C = 0 ist, sind keine Fehler erlaubt, je größer C, desto weicher die Margin und desto mehr Fehler sind erlaubt. Dies bedeutet eine Erhöhung des Bias bei gleichzeitiger Senkung der Varianz.
Die Form der Entscheidungsgrenze kann mit Hilfe der verschiedenen Kernels bestimmt werden. Hier finden sich Beispiele für alle Anwendungsmöglichkeiten von SVM in Scikit-Learn.
Naïve Bayes
Naïve Bayes Modelle sind verschiedene Klassifikatoren, die auf dem Bayes Theorem basieren. Sie finden Anwendung in der binären und Mehrklassen-Klassifizierung, sehr populär sind sie in der Textanalyse.
Die Klassifikatoren unterscheiden sich in den Annahmen, die sie zur Bedingten Wahrscheinlichkeit (Conditional Probability) P(xi|y) machen. Der Gaussian Naïve Bayes Classifier beispielsweise nimmt eine Normalverteilung der Variablen an.
Der Ausdruck ‚Naïve‘ wird verwendet, weil davon ausgegangen wird, dass die Variablen im Datensatz komplett unabhängig voneinander sind und ihr Einfluss auf das Target gleich groß ist, was bedeutet, dass alle gleich gewichtet werden. Dies ist eine Annahme, die in der Realität kaum erfüllt wird, da Variablen oft zum Beispiel miteinander interagieren. Dennoch funktioniert die Methode überraschend gut.
NB kann auch als generatives Modell verwendet werden, um neue Instanzen zu erzeugen.
Die Repräsentation von Naïve Bayes ist in der Form von Wahrscheinlichkeiten. Ein trainiertes Modell speichert eine Liste von Wahrscheinlichkeiten, bestehend aus den Wahrscheinlichkeiten für die Klassen im Trainingssatz und den Bedingten Wahrscheinlichkeiten einer jeden Variable für jede Klasse.
Das Training eines NB geht sehr schnell vonstatten. Dies liegt daran, dass nur die Wahrscheinlichkeit jeder Klasse und die Wahrscheinlichkeit jeder Klasse mit verschiedenen Eingabewerten berechnet werden müssen. Es werden hier keine Koeffizienten in einem Optimierungsprozess angepasst.
Die Wahrscheinlichkeit für eine Klasse berechnet sich einfach aus der Anzahl der Beobachtungen, die zu jeder Klasse gehören geteilt durch alle Beobachtungen. Bei einem binären Klassifizierungsproblem mit ausgeglichenen Klassen ist die Wahrscheinlichkeit für jede Klasse gleich 0,5. Die bedingten Wahrscheinlichkeiten sind die Häufigkeiten jedes Wertes einer Variablen für eine Klasse geteilt durch die Häufigkeit von Beobachtungen dieser Klasse.
Mit einem Gaußschen Naïve Bayes Modell ist das Training noch einfacher, da nur Mittelwerte und Standardabweichung von Eingabevariablen für jede Klasse berechnet werden müssen. Die NB können Signal und Rauschen gut unterscheiden und auch mit einem kleinen Trainings-Datensatz können gute Ergebnisse erzielt werden. Der Algorithmus hat keine Probleme mit fehlenden Werten, da die Variablen getrennt verarbeitet werden, sowohl im Training als auch bei der Vorhersage. Zudem ist er gut für das Online Learning geeignet, da die Wahrscheinlichkeiten mit neuen Daten einfach aktualisiert werden. Die Wahrscheinlichkeiten der Zugehörigkeit zu einer Klasse, die ausgegeben werden, müssen kalibriert werden.
Im Preprocessing müssen die Daten nicht skaliert werden, aber hoch korrelierende Variablen sollten aussortiert werden. Es könnte auch sinnvoll sein, Ausreißer, die mehr als 3 Standardabweichungen entfernt liegen, zu entfernen. Eine Log-Transformation kann helfen, die bei den Berechnungen entstehenden sehr kleinen Zahlen zu transformieren, was ansonsten zu Ungenauigkeiten führen könnte. Die kleinen Zahlen kommen daher, dass Wahrscheinlichkeiten oft sehr kleine Zahlen sind und da diese miteinander multipliziert werden, um die bedingten Wahrscheinlichkeiten zu berechnen, werden die Ergebnisse noch kleiner. Dies kann problemlos erfolgen, da die Wahrscheinlichkeiten nur qualitativ und nicht quantitativ miteinander verglichen werden (Suche nach der größeren Wahrscheinlichkeit).
In Scikit-Learn kann zwischen verschiedenen Varianten gewählt werden, um den Annahmen für verschiedene Wahrscheinlichkeitsverteilungen gerecht zu werden.
Der Umgang mit unausgeglichenen Datensätzen
Bei der binären und der Mehrklassen- Klassifizierung kommt es häufig vor, dass nicht alle Klassen gleich stark repräsentiert sind, das heißt, Instanzen mit einem Label kommen viel häufiger vor, als die des oder der anderen Labels.
Einige Beispiele für Aufgaben, bei denen eine ungleichmäßige Verteilung der Klassen zu erwarten ist, ist die Betrugsaufdeckung (Fraud Detection) bei Banktransaktionen, bei denen nur ein sehr geringer Anteil der Transaktionen als verdächtig gelten. Auch das Detektieren seltener Krankheiten in der Bevölkerung, Churn Analysen, Kreditvergaben bei Banken und Spam-Klassifizierungen haben unausgeglichene Datensätze als Grundlage.
Für einige Machine Learning Algorithmen ist es mitunter schwierig, die unterrepräsentierten Klassen zu lernen, was bedeutet, dass sie dazu tendieren, ausschließlich die überrepräsentierte Klasse vorherzusagen.
Um Fehler dieser Art zu vermeiden und die Performance des Klassifikators zu erhöhen, gibt es verschiedene Ansätze und Methoden.
Liegt ein unausgeglichener Datensatz vor, sollte zunächst nach der Ursache für die Verteilung geforscht werden, um sicherzustellen, dass es sich um eine natürliche und erwartete Ungleichheit handelt und nicht um ein Artefakt des Datensammlungs-Prozesses. Stellt sich heraus, dass die Ursache eine nicht repräsentative Stichprobe ist, sollten mehr Daten gesammelt werden oder eine andere Stichprobe (Stratifizierung) aus der Population genommen werden.
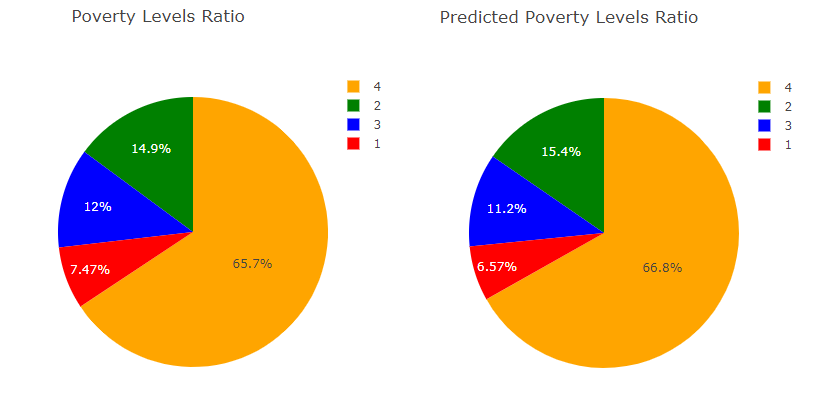
Beispiel aus dem Projekt Ein Vorhersagemodell für Armut in Costa Rica: Es gibt vier Wohlstands- bzw. Armutsklassen. Dabei ist die Klasse 4 häufiger anzutreffen, als die anderen drei Klassen zusammen. Hier sollte daher darauf geachtet werden, dass der Klassifikator die anderen Klassen, vor allem Klasse 1, auch gut lernen kann. Vergleich der Wahrscheinlichkeitsverteilung von Train und Vorhersage, um zu sehen, ob die Minderheitsklassen gut gelernt wurden.
In vielen Fällen ist es nicht mehr möglich, mehr Daten zu erhalten und in den Datensatz zu integrieren, hier können folgende Ansätze helfen:
Regularisieren. Beispielsweise kann anstatt der Logistische Regression eine Verwendung von Elastic Net, der eine Kombination aus L1 und L2 darstellt.
Gradient Boosting ist aufgrund seiner Lernmethode gut für die Modellierung unausgeglichener Datensätze geeignet. Der Prozess läuft hier sequentiell ab, jedes Mal, wenn eine falsche Vorhersage gemacht wurde, wird der Fokus auf die falsch vorhergesagte Beobachtung gelegt.
Anpassung der Schwellenwerte. Mit den (kalibrierten) Wahrscheinlichkeiten für jede Klasse die Klassifizierung manuell mit verschiedenen Schwellenwerten durchführen
Experimentieren. Andere Herangehensweise ausprobieren. One Class Prediction oder Anomaly Detection bzw. Change Detection testen.
Resampling durch Over- oder Undersampling. Die Anzahl der Instanzen jede Klasse so anpassen, dass sie ausgeglichen sind. Beim Undersampling werden Instanzen der überrepräsentierten Klasse entfernt. Beim Oversampling werden synthetische Instanzen dem Trainingsdatensatz hinzugefügt.
Bei der Arbeit mit einem unausgeglichenen Datensatz bedenken:
· Keine der genannten Methoden wird immer die besten Ergebnisse bringen, weswegen es am besten ist, verschiedene Ansätze zu testen oder zu kombinieren.
· Die Aufteilung des Datensatzes in einen Trainings- und einen Testdatensatz sollte immer stratifiziert (Hyperparameter bei Train-Test-Split) durchgeführt werden, um Instanzen jeder Klasse in jedem Set zu haben. Bei der Kreuzvalidierung Stratified Sampling verwenden, damit in jedem Fold alle Klassen repräsentiert sind.
· Die Auswahl der Metrik anpassen. Niemals Accuracy verwenden, siehe Accuracy Paradox. Stattdessen lieber die Confusion Matrix verwenden, um zu sehen, wie gut die Klassen vorhergesagt wurden Bei der Verwendung des F1-Scores in der Kreuzvalidierung den Parameter für die Berechnung des Mittelwertes auf micro setzen
· Für Visualisierungen statt der ROC besser die Precision-Recall Kurve verwenden (Artikel in Nature)
Resampling Methoden
Beim Oversampling werden dem Datensatz Instanzen der unterrepräsentierten Klasse hinzugefügt. Verwendet werden können hierfür Random Oversampling, SMOTE oder ADASYN.
SMOTE (Synthetic Minority Over-Sampling Technique) ist eine Oversampling Methode, die künstlich neue Instanzen der unterrepräsentierten Klasse kreiert. Statt Instanzen zu wiederholen, werden ähnliche Instanzen generiert, um ein Overfitting zu vermeiden. SMOTE findet die N-nächsten Nachbarn der unterrepräsentierten Klasse für jede Instanz der Klasse. Dann zieht es eine Linie zwischen den Nachbarn und generiert zufällige Punkte auf dieser Linie.
ADASYN ist eine verbesserte Version von SMOTE. Nach dem Erstellen der neuen Instanzen fügt es zufällig kleine Werte zu den Punkten hinzu. Damit sind nicht alle Samples linear korreliert mit den Elterninstanzen, sondern haben etwas mehr Varianz.
Undersampling entfernt Instanzen der überrepräsentierten Klasse. Eine Methode hierfür ist Random Undersampling. Der Nachteil beim Undersampling liegt auf der Hand, es gehen damit wertvolle Daten verloren. Undersampling der häufigeren Klasse kann verwendet werden, wenn sehr viele Daten zur Verfügung stehen. Oversampling verwenden, wenn dies nicht der Fall ist. Es kann auch eine Kombination beider Methoden angewendet werden.
Resampling Methoden werden immer nur auf den Trainingsdatensatz angewendet!
Wenn eine der Resampling Methoden verwendet wird für Datensätze, bei denen die unausgeglichene Verteilung der Realität entspricht, wird dem Lernalgorithmus eine falsche Repräsentation der Realität gegeben. Daher sollte Resampling immer mit Bedacht angewandt werden und andere Methoden zuerst getestet werden.
Fehlertypen bei der Klassifizierung
Bei der binären Klassifizierung wird zwischen Fehlern vom Typ I und vom Typ II unterschieden. Typ I bedeutet Falsch Positiv, die Klasse 1 wurde irrtümlich zugewiesen und Typ II steht für Falsch Negativ, hier wurde die Klasse 0 fälschlicherweise zugewiesen. Die unterschiedlichen Fehlertypen können mit Methoden wie der Confusion Matrix oder ROC-Kurven angezeigt werden.
Bei vielen Aufgaben ist es so, dass die beiden Fehlertypen unterschiedliche Kosten verursachen. Hier kann das Modell so angepasst werden, dass die Fehler eines Typs auf Kosten des anderen Fehlertyps zu verringern (Trade-off). Dies geschieht durch das Verschieben des Schwellenwertes, anhand dessen die Klasse zugewiesen wird. Ein Beispiel hierfür wäre das Erkennen von gefährlichen Krankheiten in einem Screening. Hier würde man eine hohe Anzahl von Falsch Positiven in Kauf nehmen, um sicher sein zu können, dass man alle Wahr Positiven gefunden hat, da die Kosten für das Nicht auffinden der Krankheit für Patienten sehr hoch sein werden.
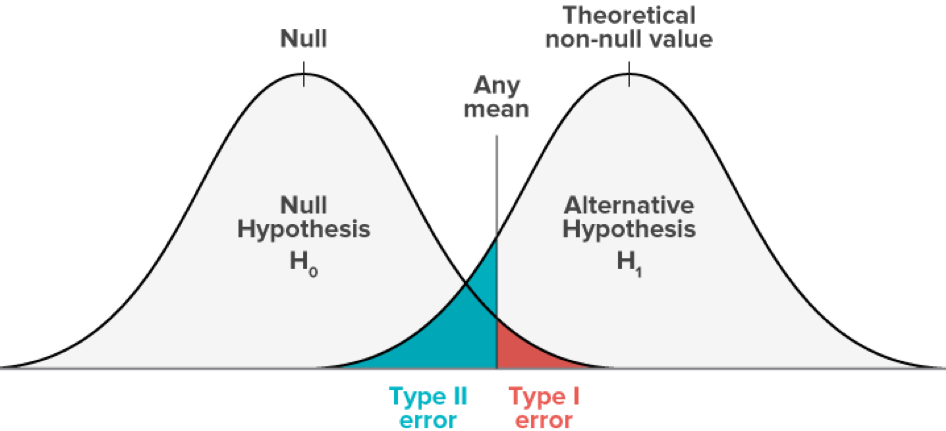
Der Trade-off zwischen Falsch Positiv und Falsch Negativen Fehlern. Bildquelle
Metriken
Die Entwicklung des lernenden Systems läuft beim überwachten Lernen über eine konstruktive Feedback-Schleife ab. Das Modell wird aufgebaut und dann anhand einer Metrik getestet. Anpassungen und Verbesserungen werden eingebracht und wieder getestet. Die Schleife reicht bis in das Data Cleaning zurück, wo die ersten Entscheidungen getroffen wurden, beispielsweise über die Art des Einsetzens fehlender Werte. Da die Metrik eine Aussage über die Qualität des Modells in jeder Stufe macht, ist es von großer Bedeutung, sie passend auszuwählen. Bei jedem Experiment, das durchgeführt wird, um den besten Lernalgorithmus, die beste Hyperparameter-Kombination und die beste Zusammenstellung der Daten zu finden, wird die Auswahl anhand des Scores der Metrik gemacht.
Die meisten Metriken sind für die binäre Klassifikation vorgesehen. Dazu gehören beispielsweise der F1-Score oder der ROC-AUC Score. Bei diesen Metriken wird die korrekte Zuordnung der positiven Klasse evaluiert. Für eine Ausweitung der Evaluierung auf Mehrklassen-Aufgaben werden diese wie eine Ansammlung von binären Aufgaben behandelt. Der Score der Evaluierung kann für jede Klasse separat ausgegeben werden oder gemittelt werden, um nur einen Score zu erhalten.
In Scikit-Learn kann über einen Parameter bestimmt werden, wie die Scores gemittelt werden sollen.
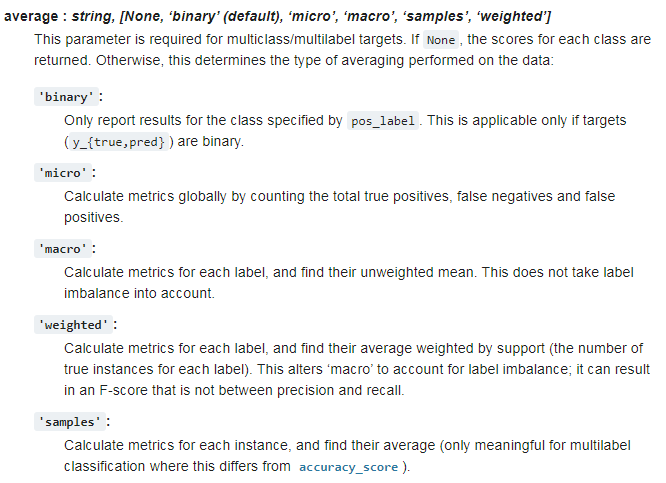
Vorgabe für die Berechnung des Mittelwertes für den F1-Score.
Accuracy
Die Accuracy berechnet sich aus der Ration der richtigen Vorhersagen zu allen Vorhersagen. Sie ist die einfachste und schnellste Art, einen Wert für die Güte eines Modells zu erhalten, in vielen Fällen kann sie jedoch irreführend sein, ist der Datensatz aber unausgeglichen, es also viel mehr Instanzen einer Klasse, als der anderen gibt, würde es reichen, wenn das Modell einfach immer die häufigere Klasse vorhersagt, um eine hohe Accuracy zu erreichen. Bei einem Datensatz mit Patienten, bei denen untersucht werden soll, ob sie an einer seltenen Krankheit leiden, kann eine sehr gute Accuracy erreicht werden, indem einfach alle Patienten als gesund klassifiziert werden. Bei einem Einsatz des Modells wären Auswirkungen allerdings verheerend, da kein einziger Patient, der tatsächlich an der Krankheit leidet, behandelt werden würde. Ein weiterer Grund, der gegen die Accuracy spricht, ist, dass es bei vielen Anwendungen wichtig ist, zwischen den Fehlerarten, die bei der Klassifizierung gemacht werden, unterscheiden zu können.
Im Beispiel der seltenen Krankheit wäre es sehr wichtig, zu wissen, wie viele Instanzen falsch negativ oder falsch positiv klassifiziert wurden. Während falsch positive Zuordnungen den Aufwand in der Patientenversorgung erhöhen und weitere Tests nach sich ziehen, würde ein falsch negativ möglicherweise den Tod des Patienten oder die Ansteckung weiterer Menschen bedeuten. Damit sind die Kosten für ein falsch positiv weitaus geringer als für ein falsch negativ und das Modell würde so angepasst, dass es lieber mehr falsch positive Fehler als falsch negative Fehler macht, um ethisch richtige Entscheidungen zu treffen. Für die Unterscheidung der Fehlerarten können Metriken wie die Confusion Matrix, Precision und Recall oder der F1-Score verwendet werden.
Daher sollte sie nur verwendet werden, wenn die Klassen ausgeglichen sind und die Unterscheidung zwischen den Fehlerarten irrelevant ist.
Confusion Matrix
Mit der Confusion Matrix kann die Performance eines Klassifikators zusammengefasst und die Fehlerarten auf einen Blick kenntlich gemacht werden. Statt einfach nur zu evaluieren, wie viel Prozent der Vorhersagen richtig waren, werden die Vorhersagen in Richtig Negativ, Richtig Positiv, Falsch Negativ und Falsch Positiv aufgeteilt, die von der Auswahl der Entscheidungsgrenze abhängen. Diese ist der Schwellenwert, an dem entschieden wird, ab welcher Wahrscheinlichkeit für eine Klasse eine Instanz der Klasse zugeordnet wird.
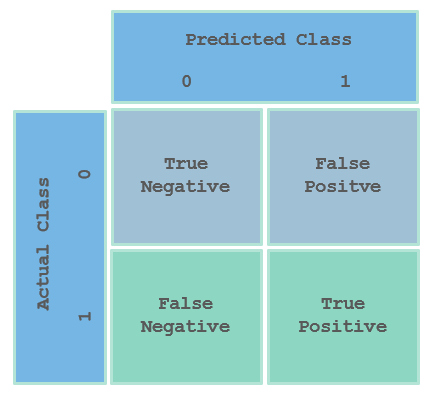
Confusion Matrix
Precision und Recall
Wie schon beschrieben, ist es oft die Aufgabe eines Klassifikators, in einem unausgeglichenen Datensatz die selten vorkommende Beobachtung zu identifizieren, die als die positive Klasse oder mit dem Label 1 bezeichnet wird. Es ist also wichtig, sicherzustellen, dass so viele wie mögliche positive Fälle identifiziert werden und Information darüber zu erhalten, wie sicher es ist, dass die als positiv eingestufte Beobachtung auch tatsächlich positiv ist. Für den ersten Fall wird die Metrik Recall verwendet, für den zweiten Fall die Metrik Precision. Die beiden Metriken stehen in einem engen Zusammenhang miteinander. Wird die Precision erhöht, verringert sich der Recall und umgekehrt (Precision/Recall Tradeoff).
Recall (True Positive Rate, Sensitivity)
Bei einem guten Recall findet der Klassifikator alle relevanten Instanzen. Recall sollte verwendet werden, wenn die Kosten für Falsch Negative sehr hoch sind. Ein Beispiel hierfür ist das Scannen von Röntgenbildern, um mögliche Tumoren zu finden. Wird ein Bild irrtümlich als frei von Tumoren kategorisiert, ist das mit sehr hohen Kosten für den Patienten verbunden.
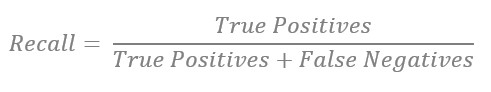
Precision
Das Modell findet nur relevante Instanzen. Eine hohe Precision bedeutet eine geringe Rate von falsch positiven Vorhersagen. Precision ist eine gute Metrik, wenn die Kosten für False Positives sehr hoch sind. Beispiel: Raketenstarts brauchen gutes Wetter. Würde man den Raketenstart bei schlechtem Wetter initiieren (Falsch Positiv), könnten die Kosten sehr hoch sein.

F1-Score
Um einen guten Ausgleich zwischen Precision und Recall zu erhalten, kann der F1-Score verwendet werden. Er berechnet sich aus dem harmonischen Mittel aus Precision und Recall.
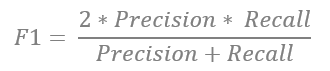
Precision-Recall Kurven
In der Precision-Recall Kurve kann für die binäre Klassifizierung die Beziehung zwischen Precision und Recall für jeden Schwellenwert abgelesen werden. Damit kann entschieden werden, welcher Schwellenwert am geeignetsten für die vorliegende Klassifizierungs-Aufgabe erscheint.
Wird der Schwellenwert nach oben verschoben, wird die Anzahl der falsch positiven Vorhersagen kleiner, bis nur noch True Positives gefunden werden. Dabei erhöht sich der Wert der False Negatives. Dies erhöht die Precision.
Wird der Threshold nach unten verschoben, erhöht sich der Recall, alle True Positives werden gefunden aber die Rate der False Positives erhöht sich ebenfalls. Precision-Recall Kurven sollten immer dann verwendet werden, wenn eine Class Imbalance vorliegt.
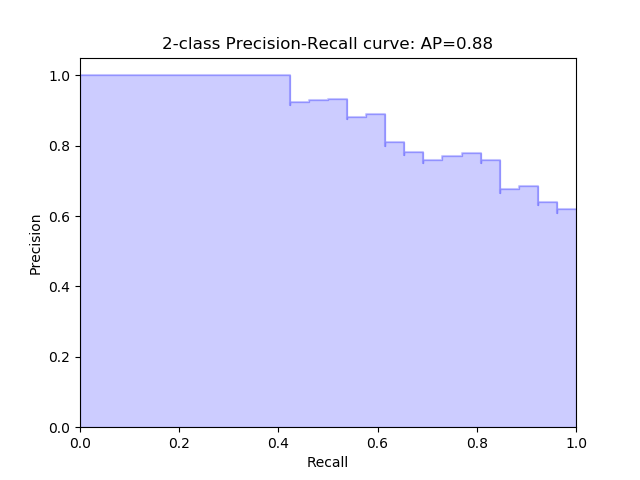
Beispiel einer Precision-Recall Kurve aus Scikit-Learn hier
Receiver Operating Characteristic Curves (ROC) und Area under the Curve (AUC)
Die ROC Kurve visualisiert die Beziehung und den Trade-Off zwischen der Falsch-Positiv-Rate und der Wahr-Positiv-Rate an den Schwellenwerten. Mit der Veränderung des Schwellenwertes nach oben steigen die Falsch-Positiv-Rate und die Wahr-Positiv-Rate an.
Der AUC ist die Fläche unter der ROC Kurve. Er misst die Performance des Klassifikators gemittelt über alle Schwellenwerte. Die Fläche unter der Kurve repräsentiert damit die Fähigkeit des Modells, zwischen positiven und negativen Klassen zu unterscheiden. Eine Fläche von 1.0 repräsentiert ein Modell, das alle Vorhersagen richtig gemacht hat. Eine Fläche von 0.5 würde einem Modell, das nicht besser als der Zufall ist, entsprechen. ROC/AUC sollte nur verwendet werden, wenn die Klassen in etwa gleichen Häufigkeiten vorkommen.
Das Beispiel ist aus Wikipedia von hier
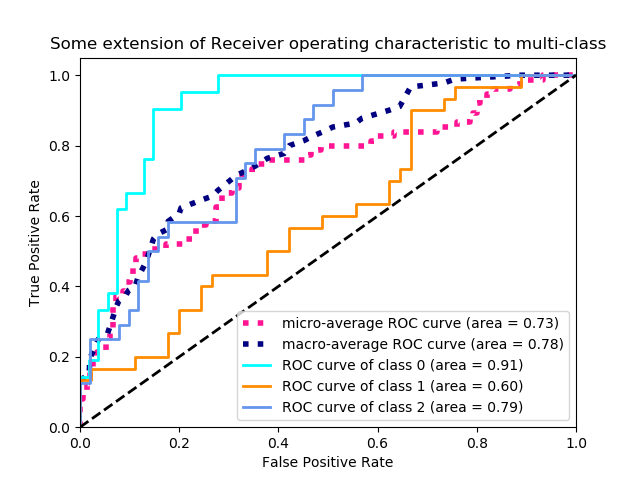
Hier ein Beispiel für die ROC Kurve einer Mehrklassen-Klassifizierung
Cohen's Kappa
Dies ist eine der besten Metriken für die Evaluierung von Mehrklassen-Klassifikatoren auf unausgeglichenen Datensätzen. Die meisten Metriken sind leicht zugunsten der häufigeren Klasse verzerrt und gehen von einer identischen Verteilung der tatsächlichen und vorhergesagten Klasen aus.
Im Gegensatz dazu misst Cohen’s Kappa die Nähe der vorhergesagten Klassen zu den tatsächlichen Klassen im Vergleich zu einer zufälligen Klassifizierung. Die Ausgabe ist normalisiert, zwischen null und 1. Je näher bei 1, desto besser der Klassifikator.
Die Kappa Statistik ist eine Metrik, die die beobachtete Genauigkeit (Observed Accuracy) mit einer erwarteten Genauigkeit (Expected Accuracy), die dem Zufall entspricht, vergleicht. Der Wert macht eine Aussage darüber, wie nahe den klassifizierten Instanzen die wahren Instanzen sind. Es können nicht nur Models mit der Ground Truth, sondern auch direkt Modelle miteinander verglichen werden.
Cohen’s Kappa ist ein guter Ersatz für die Accuracy, wenn Datensätze unausgeglichen sind.
Baselines für Klassifizierungen
Eine Baseline ist der Maßstab, anhand dessen die Performance eines Klassifikators eingeordnet werden kann.
Dies können Modelle anderer Analysten sein oder frühere Modelle, anhand derer die Aufgaben bereits zufriedenstellend gelöst wurden.
Bei Aufgaben, die Menschen traditionell gut lösen können, wie die Bilderkennung, wäre dies der natürliche Maßstab, mit der sich die Maschine messen lassen müsste. Hier spielt auch wieder die Auswahl der Metrik eine große Rolle. Eine Maschine wird wahrscheinlich nie Bilder besser als ein Mensch klassifizieren können. Dafür aber könnte sie die Bilder ebenso gut und dazu schneller und effizienter klassifizieren.
Für andere Aufgaben, bei denen Menschen größere Schwierigkeiten hätten, wie beim Durchblicken einer Tabelle mit hunderten oder gar tausenden Variablen und Millionen von Instanzen ist die Maschine klar im Vorteil und der Mensch als Maßstab nicht geeignet. Hier können künstliche Baselines verwendet werden. Bei unausgeglichenen Klassen könnte beispielweise eine Baseline verwendet werden, bei der einfach immer die häufigste Klasse vorhergesagt wird.
In Scikit-Learn gibt es für Klassifizierungen und Regressionen die Möglichkeit eine Baseline, mit dem Dummy Klassifikator zu erzeugen.
Lernkurven
Mit einer Lernkurve wird die Verbesserung der Performance eines Modells mit steigender Erfahrung visualisiert.
Dabei gibt es verschiedene Möglichkeiten, Performance und Erfahrung anzugeben. Auf der x-Achse wird Zeit oder Erfahrung dargestellt, auf der y-Achse die Verbesserung. Die Verbesserung ist eine Erfolgseinheit, wie der Fehler oder der Score einer Metrik, die Erfahrung eine Zeiteinheit, wie zum Beispiel die Anzahl von Instanzen, die verarbeitet wurden. Wird der Loss als Maß der Verbesserung verwendet, anhand dessen das Model optimiert wird, so spricht man von einer Optimization Learning Curve. Wird hingegen eine Evaluierungsmetrik, wie zum Beispiel die Accuracy verwendet, ist das Ergebnis eine Performance Learning Curve.
Die Kurve des Train Datensatzes zeigt, wie gut das System lernt, die Kurve des Test-Sets zeigt, wie gut es generalisieren kann. Anhand des Vergleichs der Fehler, die beim Training und auf dem Testsatz gemacht werden, können Bias und Varianz im Modell diagnostiziert werden. Je kleiner die Lücke zwischen der Fehlerkurve von Test-Set und Train-Set, desto geringer die Varianz. Je weiter weg die Fehlerkurve von der angestrebten Performance, desto größer der Bias.
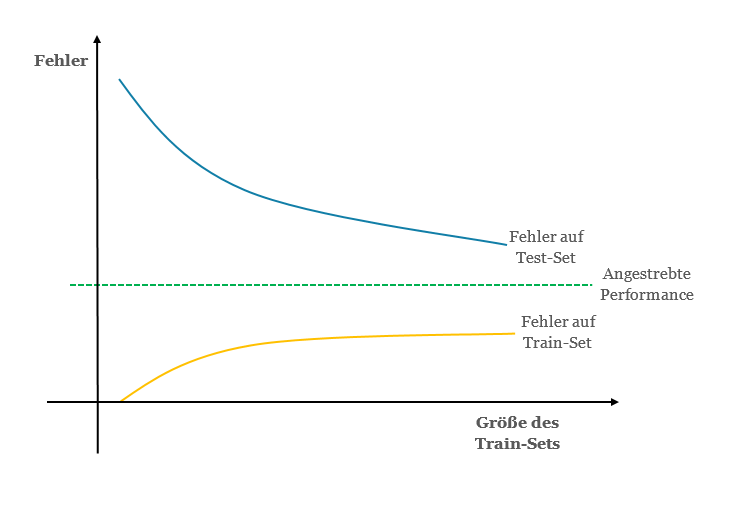
Lernkurve der Fehlerrate
Kalibrierte Wahrscheinlichkeiten
Um die Zuversicht in eine Vorhersage ausdrücken zu können, kann für jede Instanz die Wahrscheinlichkeit der Zugehörigkeit einer Klasse, anstatt der Klasse ausgegeben werden. Damit kann in Machine Learning Systemen eine Verschleppung von Fehlern verhindert werden und durch eine Anpassung des Schwellenwertes die Zuweisung zu Klassen angepasst werden.
Vorhergesagte Wahrscheinlichkeiten, die zur erwarteten Verteilung von Wahrscheinlichkeiten für jede Klasse passen, werden als kalibriert (Calibrated) bezeichnet. Bei kalibrierten Klassifikatoren kann der Output in Scikit-Learn mit der Funktion „predict_proba“ als Konfidenzniveau (Confidence Level) interpretiert werden.
Die Logistische Regression gibt kalibrierte Vorhersagen zurück, da es Log-Loss optimiert. Nicht-lineare Algorithmen, wie Naïve Bayes, der Random Forest Classifier oder der Linear Support Vector Classifier können die Wahrscheinlichkeiten zwar ausgeben, allerdings entsprechen sie nicht der Realität, sondern sind verzerrt und müssen daher kalibriert werden.
Eine populäre Methode zur Kalibrierung sind Reliability Diagrams, auch Calibration Curves genannt, mit deren Hilfe Ausgaben aus dem Modell diagnostiziert und gegebenenfalls angepasst werden kann. Dafür werden die tatsächlich beobachten Verteilung jeder Klasse im Datensatz verwendet.
Die Kalibrierung sollte nicht auf dem Datensatz, der für das Fitting verwendet wird, stattfinden, sondern auf neuen Daten.
In Scikit-Learn können Calibration Curves für einen binären Klassifikator mit dem Modul sklearn.calibration.calibration_curve erzeugt werden.
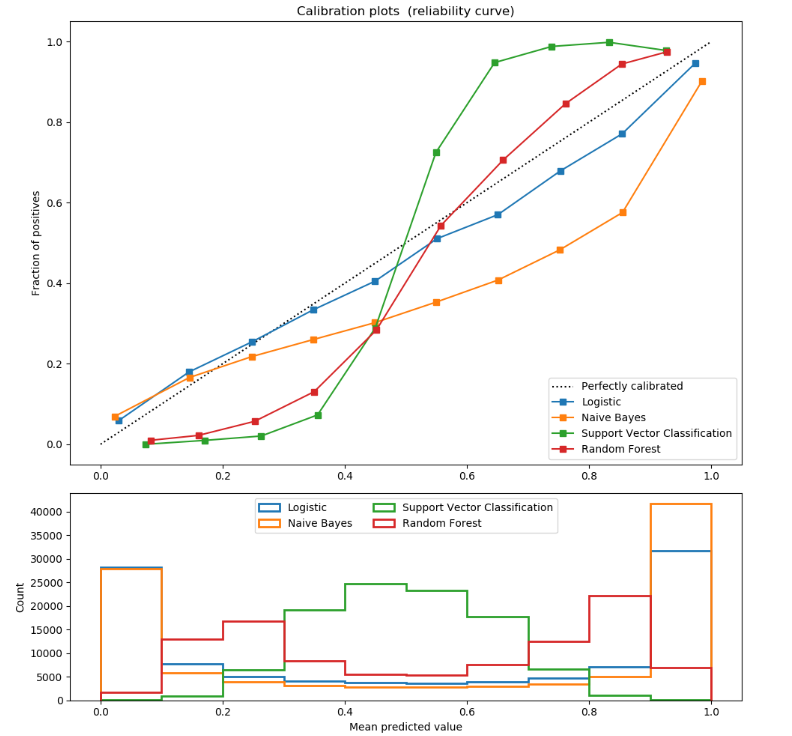
Der Vergleich der Calibration Curves mehrerer Klassifikatoren mit Scikit-Learn und Matplotlib. Code hier.
Konfidenzintervalle
Im Machine Learning wird das Konfidenzintervall verwendet, um das Vertrauen in die Abschätzung des Scores eines Vorhersage-Modells anzugeben.
Konfidenzintervalle kommen aus dem Feld der Estimation Statistics. Diese ist eine Ansammlung von Methoden, die verwendet werden, um die Größe von Effekten und Unsicherheiten für Schätzwerte zu quantifizieren.
Das Konfidenzintervall besteht aus zwei Komponenten, den beiden Grenzwerten des Bereichs und der Wahrscheinlichkeit, dem Konfidenzniveau γ, dass der Score innerhalb dieser Grenzen fallen wird.
Meistens wird dafür ein Konfidenzniveau von y = 95% gewählt. Es kann dabei davon ausgegangen werden, dass je größer die Stichprobe ist, die für die Abschätzung verwendet wurde, desto schmaler der Bereich des Konfidenzintervalls, und je schmaler der Bereich, desto präziser die Schätzung.
Die Interpretation von Klassifikatoren
Neben der Evaluierung eines Klassifikators ist seine Interpretation wesentlich für das Verständnis und die Optimierung eines Machine Learning Modells. Hier wird festgestellt, wie der Klassifikator lernt und wie er Signal und Rauschen im Datensatz unterscheidet. Dafür wird untersucht, welchen Wert das Modell den einzelnen Features (Feature Importance) beim Fitten zugemessen hat. Je stärker die Beziehung eines Features zum Target, desto höher sollte es vom Modell eingeschätzt werden.
Bei Lernalgorithmen, die auf Bäumen basieren, so wie Random Forest, können die Feature Importances nach dem Training direkt angegeben werden. Hier sollte allerdings darauf geachtet werden, dass das Modell von kollinearen Features verwirrt werden kann.
Bei parametrischen Algorithmen, wie der Logistischen Regression, können die Features anhand der Koeffizienten der linearen Funktion interpretiert werden. Je höher das Gewicht, dass das Modell dem Feature zugemessen hat, desto wichtiger das Feature.
Bei komplexeren Modellen, wie Neuronalen Netzen, ist eine direkte Interpretation nicht mehr möglich. Hier können Post-Hoc Methoden angewandt werden, die das Modell im Nachhinein untersuchen. Hierfür können Algorithmen wie die Permutation Feature Importance oder LIME (Local Interpretable Model-Agnostic Explanations) verwendet werden. Mehr zum Thema im Artikel Interpretation.
Ablauf einer Klassifizierung
- Ziel, Metriken und Baseline festlegen
- Exploration und Bereinigung des Datensatzes
- Das Feature Engineering (mehr dazu im Artikel Feature Engineering)
- Preprocessing der Daten (Resampling, Encoding)
- Den Datensatz aufteilen in einen Trainings- und einen Testdatensatz
- Testen mehrerer Lernalgorithmen in einer Kreuzvalidierung und Auswahl des passendsten Algorithmus
- Hyperparameter-Tuning für den gewählten Lernalgorithmus
- Testen verschiedener Variationen des Trainingssatzes aus dem Feature Engineering
- Kalibrierung
- Konfidenzintervalle berechnen oder durch Bootstrapping ermitteln
- Interpretation des Modells
- Dokumentieren und Visualisieren der Ergebnisse
