Feature Engineering
Photo by Sebastian Unrau on Unsplash
Einführung
Die Grundlage jedes erfolgreichen Machine Learning Projekts ist eine präzise Repräsentation der Realität anhand von Daten. Diese Daten sind die Informationseinheiten, die die Realität abbilden und aus denen der Lernalgorithmus, die zugrundeliegende Wahrheit (Target Function) approximiert.
Dies ist der Grund, warum ein Modell immer nur so gut sein kann, wie die Daten, aus denen es erzeugt wurde. Ist die Datengrundlage nicht gut, weil Attribute fehlen, fehlerbehaftet sind oder ein Bias aufweisen, hat auch der beste und eleganteste Lernalgorithmus keine Chance, ein nützliches Modell aufzubauen.
Beim Feature Engineering werden die vorhandenen Variablen, die Features, so optimiert, dass sie die bestmögliche Repräsentation der Realität erlauben. Dafür werden wichtige Attribute und Muster herausgestellt und irrelevante oder redundante Informationen entfernt.
Nicht alle der vorhandenen unabhängigen Variablen im Datensatz sind für die Vorhersage der abhängigen Variablen gleich hilfreich. Neben einigen, die eine starke Beziehung mit dem Target habe, gibt es Prädiktoren, die nur einen geringen oder überhaupt keinen Einfluss auf dieses haben. Die Stärke eines Features, die das Modell einem Feature beimisst, wird Feature Importance genannt. Je höher die Feature Importance, desto wichtiger ist das Feature für die Vorhersage.
Dabei gilt nicht, je mehr Daten im Modell desto besser, sondern Occam’s Razor. Das beste Modell kann so viele Informationen wie möglich mit so wenigen Daten wie nötig darstellen. Je einfacher ein Modell, desto besser kann es interpretiert werden und desto weniger tendiert es dazu, überangepasst zu sein, was dazu führen würde, dass es schlechter generalisieren kann. Weniger Daten bedeuten auch eine Ersparnis von Ressourcen wie Rechenzeit und Speicherplatz. Sind die Features gut gewählt, kann anstelle von komplexeren Lernalgorithmen auf einfachere zurückgegriffen werden, was Interpretierbarkeit und Geschwindigkeit des Modells verbessert.
“Coming up with features is difficult, time-consuming, requires expert knowledge. ‘Applied machine learning’ is basically feature engineering.”

Der Beitrag einer Variablen
Ein gutes Feature zeichnet sich dadurch aus, dass es eine starke Beziehung mit dem Target hat. Für die objektive Beurteilung dieser Beziehung zwischen Prädiktor und Zielvariablen gibt es verschiedene Methoden. Es kann zum einen ein einfaches und transparentes Modell verwendet werden, bei dem die Koeffizienten der Variablen ihrer Bedeutsamkeit entsprechen. Sollen komplexere Lernalgorithmen verwendet werden, können diese nach dem ersten Training interpretiert werden, um herauszufinden, wie das Modell die Variablen eingeschätzt hat. Dafür können Ansätze wie die Permutation Feature Importance oder ausgefeilter Methoden wie LIME oder SHAP verwendet werden.
Um eine erste Abschätzung vorzunehmen, kann bereits bei der Exploration der Daten eine Korrelationsmatrix nach Pearson erstellt werden, um erste Ideen für das Feature Engineering zu bekommen.
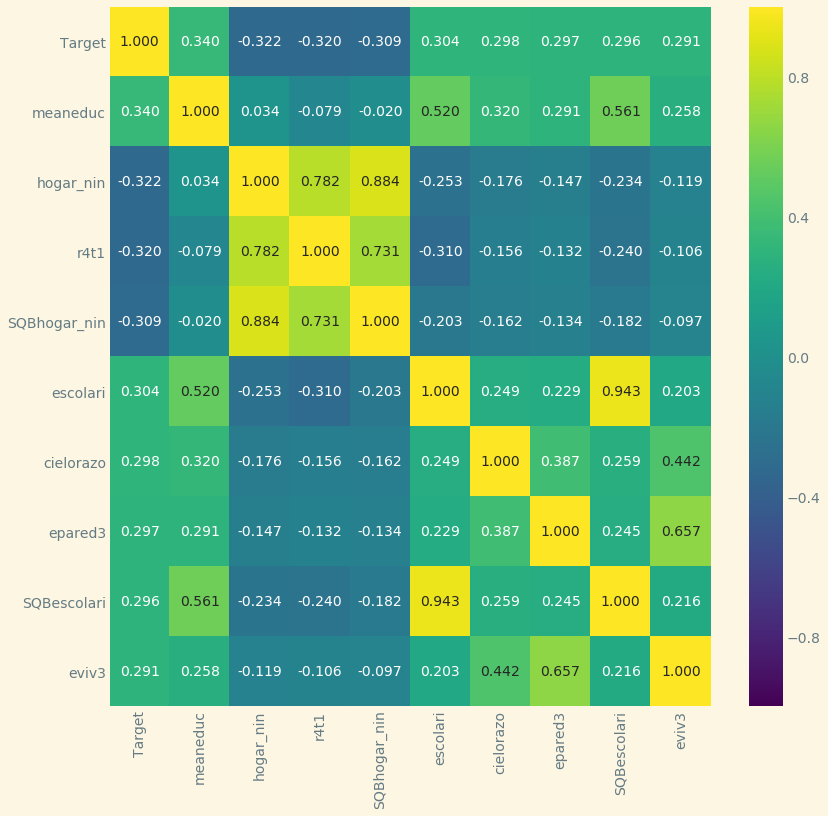
Lernalgorithmen, die auf Entscheidungsbäumen basieren, wie das Random Forest Ensemble, können Feature Importances direkt ausgeben.
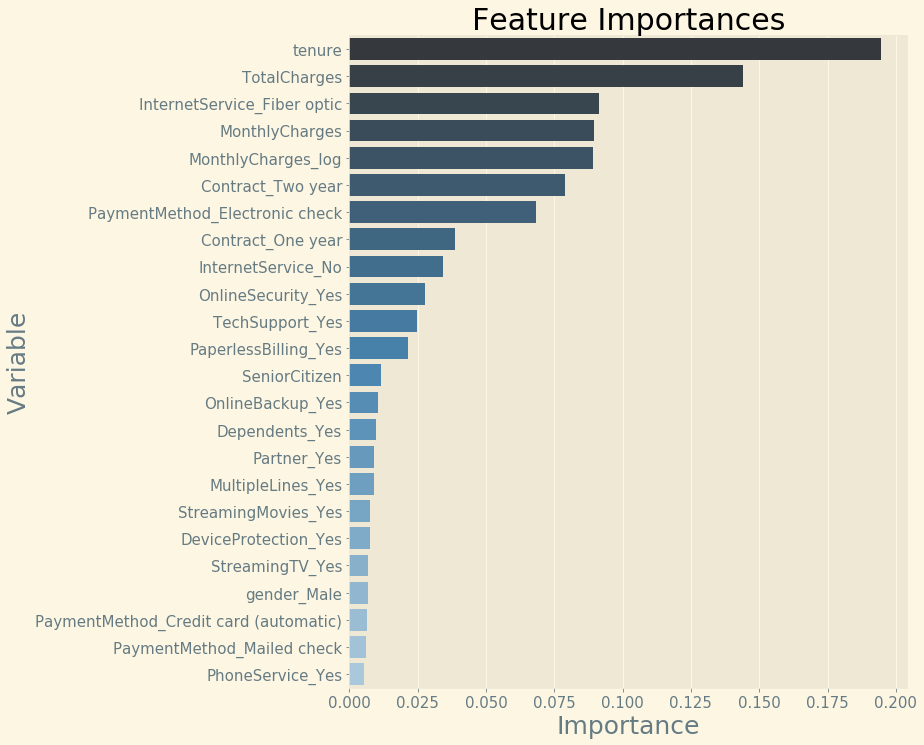
Aus dem Projekt Telco Customer Churn: Features Importances mit Random Forest und Matplotlib
Dimensionsreduktion
Ein bekanntes Problem ist die kombinatorische Explosion oder der „Fluch der Dimensionalität„, ein Begriff, der in den 50er Jahren von Richard Bellman geprägt wurde. Dieser sagt aus, dass wenn sich die Zahl der Dimensionen erhöht, dass sich gleichzeitig die Anzahl der für eine gute Repräsentation benötigten Beobachtungen exponentiell erhöht. Wenn also beispielsweise 20 Boolesche Features in einem Datensatz vorhanden sind, bedeutet das mehr als eine Million verschiedener möglicher Kombinationen. Damit ein Modell gut lernen kann, bräuchte es mindestens ein Beobachtungsbeispiel jeder dieser möglichen Kombinationen. Da oft nicht genug Daten vorhanden sind, um dieser Anforderung zu genügen, sollten die Features beschränkt werden.
Bei der Dimensionsreduktion wird die Anzahl der Features im Datensatz verkleinert, ohne dass dabei wesentliche Informationen verloren gehen.
Das Ausfiltern irrelevanter oder redundante Daten minimiert das Rauschen in den Daten und verbessert die Generalisierungsfähigkeit des Modells, während die Interpretation erleichtert wird und sich Rechenzeiten und Ressourcenaufwand verringern.
Der Ablauf ist zweistufig. In der ersten Stufe, der Feature Selection werden Features aus dem Datensatz ein- oder ausgeschlossen, ohne diese selbst zu verändern, in der zweiten Stufe dann, der Feature Extraction werden neue Features durch eine Kombination der vorhandenen Features erzeugt, um diese dann zu ersetzen.
Feature Selection
Bei der Feature Selection wird zwischen drei Ansätzen unterschieden; Filter, Wrapper und Embedded Methoden.
Die Filter Methoden verwenden statistische Methoden für die Evaluierung von Features, Wrapper Methoden funktionieren empirisch und Embedded Methoden stellen einen Bestandteil eines Lernalgorithmus dar.
Bei den Filter Methoden werden univariate statistische Analysen verwendet, um die Eigenschaften eines Features zu evaluieren, beispielsweise der Korrelationskoeffizient nach Pearson oder Spearman, oder der Chi-Quadrat Test.
Eine weitere Methode ist die Verwendung des Variance Thresholds. Diese begründet sich auf der Tatsache, dass Variablen mit einer höheren Varianz mehr Informationen beinhalten. Dafür wird die Varianz aller Features berechnet und diejenigen, die unter einem bestimmten Schwellenwert liegen, werden ausgeschlossen.
Wrapper Methoden messen die Performance verschiedener Feature-Sets in einer Kreuzvalidierung und nutzen diese, zum Auffinden und Eliminieren von irrelevanten Features. Ein Beispiel hierfür ist die Recursive Feature Elimination.
Dafür wird das Model zunächst mit allen Features gefittet, um dann in mehreren Iterationen jeweils das schwächste Feature zu entfernen. Die Iterationen laufen, bis eine zuvor festgelegte Anzahl von Features erreicht wird.
Embedded Methoden sind Wrapper Methoden, die in Algorithmen integriert sind. Zu den Algorithmen, die Wrapper Methoden verwenden, gehören solche, die auf Entscheidungsbäumen basieren und regularisierte Regressionsalgorithmen wie Lasso Regression, Ridge Regression und Elastic Net.
Für die Auswahl von Features Sets sind Wrapper und Embedded Methoden ideal, weil sie sehr zuverlässig sind. Andererseits brauchen Filter Methoden viel weniger Rechenzeit, da kein Training stattfindet.
Aus diesem Grund würden sich bei einer Anwendung, bei der Modelle online trainiert werden, Filter Methoden anbieten. Auch wenn eine Begründung geliefert werden soll, warum Features ein- oder ausgeschlossen wurden, sind Filtermethoden dem „Brute-Force“- Ansatz der Wrapper Methoden überlegen, da sie interpretierbar sind. Es hängt also immer von den Anforderungen und dem Einsatzgebiet ab, welche der Methoden vorzuziehen ist.
Feature Extraction
Mit Hilfe der Feature Extraction werden mehrere Features zu einem Feature kombiniert, das deren Information beinhaltet. Dies kann entweder von Hand durchgeführt werden oder mit der Hilfe von Methoden wie der Hauptkomponentenanalyse oder einer Linearen Diskriminanzanalyse. Bei Bilddaten geschieht können Features beispielsweise durch Detektieren von Linien oder Kanten reduziert werden, hierfür kommt beispielsweise die Einzelwertzerlegung Methode zum Einsatz.
Die Hauptkomponentenanalyse (Principal Component Analysis, PCA)
Bei der PCA wird eine Matrix mit n Features in eine Matrix mit weniger als n Features konvertiert, ohne dabei Information zu verlieren. Dies geschieht unüberwacht durch das Erzeugen von linearen Kombinationen der ursprünglichen Features. Dann werden die dadurch entstandenen Komponenten nach ihrer Explained Variance bewertet und sortiert. Die erste Komponente (First Principal Component) erklärt den größten Anteil der Varianz des Datensatzes, die zweite Komponente die zweitmeiste, und so weiter. Mit der Festlegung einer ‚Cumulative Explained Variance‘ wird die Anzahl von Principal Components begrenzt. Es werden die ersten k Principal Components, die 80-90 % der Variation repräsentieren, gewählt und die restlichen fallen gelassen, da sie das Model nicht signifikant verbessern.
In der Vorbereitung für eine PCA sollten die Daten immer skaliert werden, da ansonsten einfach nur die Variablen der größeren Skalen dominieren und zu Principal Components werden.
Der Vorteil einer PCA begründet sich darin, dass sie schnell und einfach zu implementieren ist. Es gibt verschiedene Variationen der PCA, mit deren Hilfe sie auf spezifische Anwendungen angepasst werden kann. Nachteilig wirkt sich aus, dass die PCA kaum zu interpretieren ist.
Lineare Diskriminanzanalyse (LDA)
Die LDA ist im Prinzip der PCA sehr ähnlich, beide suchen nach denjenigen linearen Kombinationen der Variablen, die die Daten am besten erklären können. Sie läuft jedoch im Gegensatz zur PCA überwacht ab und benötigt eine Matrix aus kontinuierlichen unabhängigen Variablen und einer kategorischen abhängigen Variablen. LDA maximiert nicht die Explained Variance, sondern fokussiert sich auf die Maximierung der Trennbarkeit von bekannten Kategorien. Dies geschieht durch das Generieren einer neuen Entscheidungsgrenze, auf die die Datenpunkte projiziert werden. Diese wird so gelegt, dass die Trennbarkeit der Daten maximiert wird.
Bei der Anwendung von LDA wird davon ausgegangen, dass die Variablen normalverteilt sind. In der Vorbereitung sollten die Daten, wie für die PCA, skaliert werden
Autoencoder
Autoencoder sind Neuronale Netzwerke, die Datensätze komprimieren, in dem sie diese mit weniger Information reproduzieren. Der Input entspricht also dem Output und es gibt gleich viele Neuronen im Input wie im Output Layer. Die Schlüsselkomponente hierbei ist der Hidden Layer, in dem der Input komprimiert wird. Dazu versucht dieser, dieselbe Information mit einer viel geringeren Anzahl von Neuronen darzustellen. Damit werden Sparse Representations erzeugt. Wenn dieser Layer aus dem Model extrahiert wird, kann jedes Neuron als eine Variable angesehen und verwendet werden.
Autoencoder arbeiten überwacht, die Optimierung läuft über mehrere Iterationen, wobei die Verlustfunktion per Gradient Descent minimiert wird.
Ein Nachteil der Autoencoder ist, dass sie sehr viele Daten benötigen, um gut zu performen zu können.
Feature-Konstruktion
Bei der Feature-Konstruktion werden dem Datensatz neue Prädiktoren hinzugefügt.
Hierzu gibt es unzählige Möglichkeiten, dem Datensatz relevante Informationen hinzuzufügen. Hier einige Beispiele:
Beim Binning wird durch Diskretisieren eine kontinuierliche Variable in eine kategorische Variable umgewandelt. Dies kann vor allem die Performance von Lernalgorithmen, die auf Entscheidungsbäumen basieren, verbessern.
Durch Dekomposition können komplexe Features in einfachere Features aufgeteilt werden, die für sich genommen eine größere Bedeutung für die Vorhersage haben.
Beispielsweise können aus einer Spalte des Typs ‚Datetime‚ mehrere Spalten mit Tag, Monat, Jahr, Stunde und Minute erzeugt werden. Damit könnten wichtige Trends, wie saisonale oder tageszeitabhängige Veränderungen aufgespürt werden. Es gibt Situationen, in denen die Stunde oder der Wochentag eines Ereignisses relevanter als das Datum sein können, beispielsweise bei einer Analyse von Fahrtzeiten von PKW im Stadtverkehr.
Beim Hinzufügen neuer Features aus externen Quellen lohnt es sich, einen Domainexperten hinzuzuziehen, der aus Erfahrung weiß, wie die Variablen miteinander interagieren, welche Faktoren wann und wie eine Rolle spielen und welche im Datensatz herausgestellt werden sollten. Dabei sollte nicht vergessen werden, dass wir viele Dinge als selbstverständlich hinnehmen und in unserer Wahrnehmung der Welt schweigend Informationen voraussetzen, die eine Maschine nicht „wissen“ kann. Diese „versteckten Pools“ von Information können sehr wertvoll sein, und sie zu erkennen und dem Lernalgorithmus zur Verfügung zu stellen, kann das Modell bedeutend verbessern.
Kontinuierliche Variablen können in einem Schwellenwertverfahren in binäre Variablen umgewandelt werden, die die alten ersetzen oder zusätzlich als Indikator fungieren. Binäre Variable können auch fehlende Werte oder andere interessante Merkmale kennzeichnen. Dies könnte beispielsweise sinnvoll, wenn sich beim Ersetzen von fehlenden Werten zeigt, dass diese nicht zufällig verteilt waren.
Die Feature Construction wird von Hand durchgeführt, weshalb sie oft auch als Kunst bezeichnet wird.
Polynomiale- und Interaktionsterme
Ein Machine Learning Modell soll Beziehungen zwischen den Variablen lernen und aus diesen Mustern neue Vorhersagen zu generieren. Die Stärke einer Beziehung zwischen Prädiktor und Target wird als der Effekt der Variablen auf die Zielvariable interpretiert.
Der Effekt, den die unabhängigen Variablen auf die abhängige Variable haben, wird als Haupteffekt bezeichnet.
Neben diesen gibt es jedoch noch eine andere Sorte von Effekten, die Interaktionseffekte. Diese entstehen, wenn der Haupteffekt einer der Variablen im Datensatz vom Wert einer oder mehrerer anderer Variablen beeinflusst wird. Dies bedeutet jedoch nicht, dass diese Variablen miteinander korrelieren oder eine der Variablen einen Einfluss auf die andere erklärende Variable hat. Es bedeutet nur, dass eine oder mehrere erklärende Variablen einen Einfluss auf den Effekt einer anderen erklärenden Variablen auf das Target haben.
Interaktionen sind in der realen Welt oft anzutreffen und weswegen es immer sinnvoll ist, diese im Modell miteinzubeziehen. Gibt es statistisch signifikante Interaktionseffekte im Modell, können die Haupteffekte nur unter Berücksichtigung dieser korrekt interpretiert werden.
Eine einfache Möglichkeit, herauszufinden, ob zwei oder mehr Variablen miteinander interagieren, kann ein Interaktions-Plot verwendet werden. Dies ist ein einfaches Liniendiagramm. Eine weitere Möglichkeit ist die Verwendung von Entscheidungsbäume, siehe Friedmans H-Statistik und die Dokumentation von XGBoost hier. In der H-Statistik wird die Stärke der Interaktion einer Variablen mit jeweils jeder der anderen Variablen im Datensatz gefunden. Sie wird mithilfe der Varianz, die durch die Interaktion beschrieben wird, erklärt.
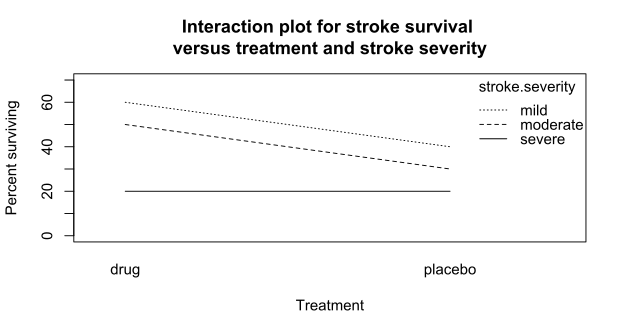
Beispiel für ein Interaktions- Plot aus Wikipedia. Sind die Linien parallel zueinander, gibt es keine Interaktion, ist die Steigung dieser allerdings unterschiedlich, und sie kreuzen sich, kann von einem Interaktionseffekt ausgegangen werden.
Um nichtlineare Beziehungen zwischen den unabhängigen und der abhängigen Variablen in einem Modell zu integrieren, können Monome höheren Grades als neue Features hinzugefügt werden, um ein Polynom höheren Grades zu erhalten. Meistens werden quadratische und kubische Monome verwendet. Der Exponent kann dabei sowohl positiv als auch negativ sein.
Lineare Algorithmen, wie Logistic Regression, können Interaktionen und kurvige Beziehungen zwischen den Variablen nicht erfassen und integrieren, hier sollten Interaktionsterme und Polynomiale Terme manuell in das Modell integriert werden.
Baumbasierte Algorithmen, wie Random Forest oder Boosted Trees dagegen, können diese Effekte erkennen und darstellen.
Bei der Verwendung des Lernalgorithmus Support Vector Machines kann ein Kernel gewählt werden, der das Modell automatisch um polynomiale Terme erweitert, um Kurven im Input-Raum abzubilden. Das resultierende Modell mit Polynomialen- und Interaktionstermen ist weiterhin linear, weil die Parameter linear sind.
Interaktionsterme werden meistens als Produktterme der Variablen erstellt, können aber auch anders abgebildet werden. Das Hinzufügen von Interaktionstermen und Polynomialen Termen fügt dem Datensatz keine neuen Variablen hinzu, sondern erhöht die Komplexität des Modells. Je komplexer das Modell, desto genauer können die Vorhersagen sein. Allerdings kann eine hohe Komplexität auch zu einer Überanpassung durch den Lernalgorithmus führen, was die Generalisierungsfähigkeit des Modells beeinträchtig.
Das Hinzufügen von Polynomialen- und Interaktionstermen kann in Scikit-Learn automatisch erfolgen. Um die Multikollinearität, die durch das Hinzufügen der neuen Terme im Datensatz entsteht, zu reduzieren, können die Variablen zuvor zentriert werden.
Automatisiertes Feature Engineering
Die fortschreitende Automatisierung von Prozessen macht auch nicht vor der Entwicklung von Machine Learning Modellen halt. Obwohl an vielen Stellen noch menschliche Kreativität und Intuition gefragt sind, können an manchen Stellen der Pipeline Algorithmen verwendet werden, die die gleiche Aufgabe mindestens so gut, wenn nicht besser können. Das manuelle Feature Engineering ist sehr aufwändig und setzt eine gute Expertise und viel Fingerspitzengefühl voraus. Es muss zudem für jeden Datensatz neu gemacht werden.
Im automatisierten Feature Engineering dagegen werden automatisch nützliche Features extrahiert und der Vorteil besteht darin, dass diese Methode auf jedes Problem angewandt werden kann. So können in wenigen Schritten tausende von Features erzeugt werden.
Eine bekannte Anwendung für das automatisierte Feature Engineering ist Featuretools, eine Open-Source Python Bibliothek. Sie verwendet eine Methode, namens Deep Feature Synthesis. Mit Hilfe von Funktionen, den Feature Primitives, werden Transformationen und Aggregationen, die als „Baublöcke“ verwendet werden können, definiert.
Aus einem Stapel mehrerer Feature Primitives wird ein Deep Feature. Je mehr Primitives, desto tiefer das Feature. Featuretools kann mit relationalen Daten, die über mehrere Tabellen verteilt sind, umgehen und fasst diese dafür zu einem Entity Set zusammen.
